Jim Loy's DCTG Diagrams
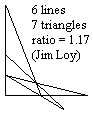
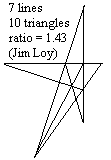
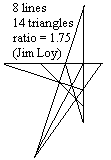
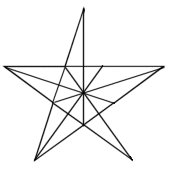 9 lines, 16 triangles, Score = 1.77
9 lines, 16 triangles, Score = 1.77
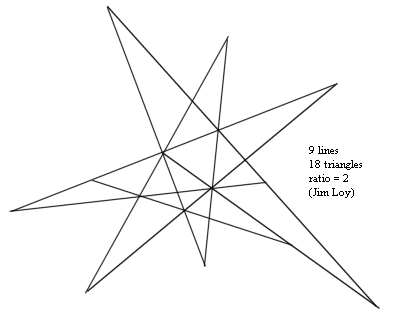
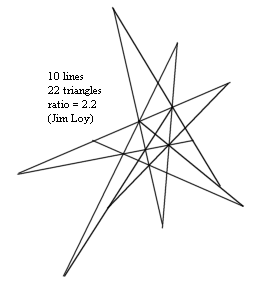
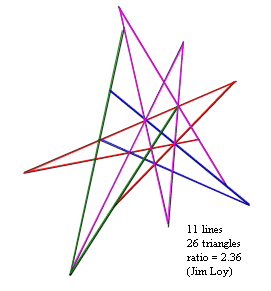
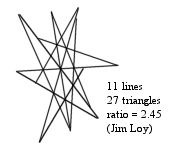
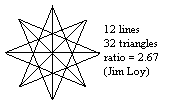
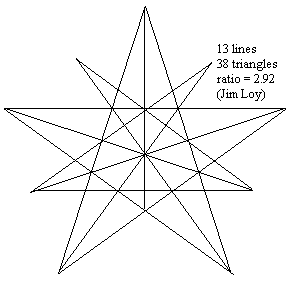
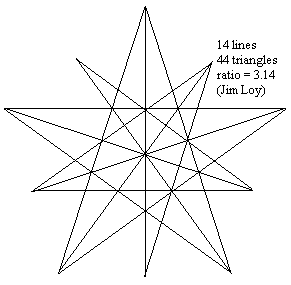

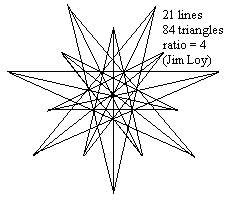
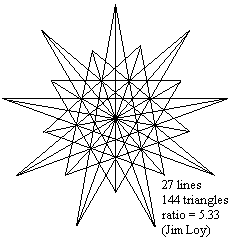

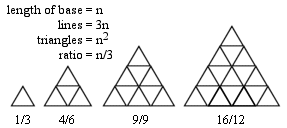
Here is a diagram which shows that you can get a ratio (as defined by the rules to the puzzle) as great as you want, without limit. I have drawn four triangles, with sides 1, 2, 3, and 4. You can draw such a triangle with any number of sides (n). The number of lines is 3n, in every case. It is not very difficult, using geometric series, to show that the number of triangles is n^2 (n squared) in every case. So the ratio is n/3. If you want a ratio of 100, then you just need a large triangle with a side of 300 units, and you would have 900 lines and 90,000 triangles.